Zar propone un bellissimo problema matematico, che ripropongo adattandolo alla stagione (di cocomeri, in giro, ce ne sono pochi).
Un piccolo risparmiatore chiama la propria banca per avere informazioni sull’andamento dei propri investimenti dopo i recenti crolli in borsa.
La banca lo rassicura: prima del crollo, egli aveva investito in azioni il 99% dei suoi averi; dopo il crollo, il valore di queste azioni è sceso al 98% del suo capitale. Il piccolo risparmiatore si complimenta con la banca per averlo consigliato così bene.
Posto 100 il capitale del piccolo risparmiatore prima del crollo, a quanto ammontano adesso i suoi risparmi?
La soluzione lascia interdetti.




Ho letto la tua spiegazione nel commento al post di Zar e mi è sembrata brillante.
Ma devo dire che questa riformulazione lo è ancor di più.
Molto attuale.
Sì, decisamente più attuale dei cocomeri… 🙂
@Weissbach: Grazie. Penso che riprenderò la spiegazione qui in un commento o aggiornamento al post.
@zar: Io, comunque, preferisco i cocomeri ai crack finanziari 😉
Bisognerebbe forse esplicitare che quell’1% di non-azioni rappresenta una quantità di capitale non-investito (ovvero che non può aumentare nè diminuire)?
Ho girato al mio panel di esperti… 😉
@hronir: io avevo pensato quell’1% come depositato su un conto corrente, che con gli elevati tassi di interesse è praticamente fermo.
@Simone Cosimi: Ecco la soluzione:
100 = capitale prima della crisi = 99 + 1 (azioni + conto corrente)
Il capitale dopo la crisi è l’incognita di una semplice equazione: il capitale è uguale alla somma depositata sul conto corrente più il 98% del capitale stesso
x = 1 + 98/100 * x
100x = 100 + 98x
100x – 98x = 100
2x = 100
x = 50
Il capitale dopo la crisi è la metà del capitale prima della crisi. Eppure è semplicemente passato dal 99% al 98%!
Nei commenti al post di zar proponevo di ragionare sulla percentuale della parte fissa (la polpa dei cocomeri o la cifra depositata sul conto). Di quanto deve diminuire il capitale affinché la cifra sul conto corrente, che rimane costante, raddoppi la propria percentuale? Messa in questi termini, è ovvio che il capitale si debba dimezzare. E infatti il risultato è lo stesso passando dal 98% al 96% e dal 96% al 92% (la percentuale della parte fissa raddoppia ogni volta).
Un grafico può aiutare:
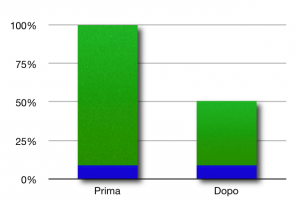
La parte blu è quella fissa, quella verde quella che cambia.